HOME PAGE
I’ve been teaching bridge-building and crane-building to middle and high school students in the Portland metro area since 1997. The kids and I have built everything from small cranes
To contact me go to info@portlandjib.com


To a crane that could lift a 140 pound kid.

This crane , with a 16ft long boom, could lift 3 kids.

We built small truss bridges.

This 12ft long arch bridge held the entire class.

The towers of this suspension bridge were 40ft apart. The bridge was rated at 4 tons.

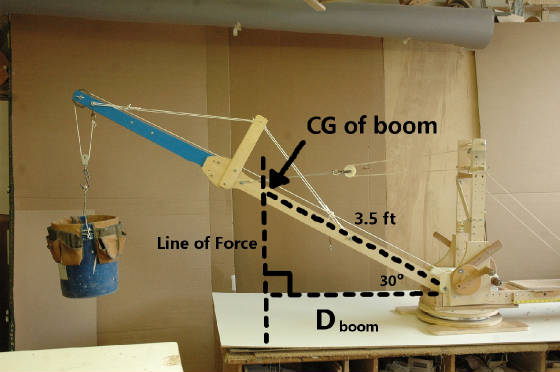
The team from the Arbor School of Arts and Sciences used this model crane to learn about torque.
They learned how to compute how much counter-weight was needed to prevent the crane from tipping over.